Math Definitions - Letter Z
Chapters
Definition of Zero (of a function)
Definition of Zero (of a function)
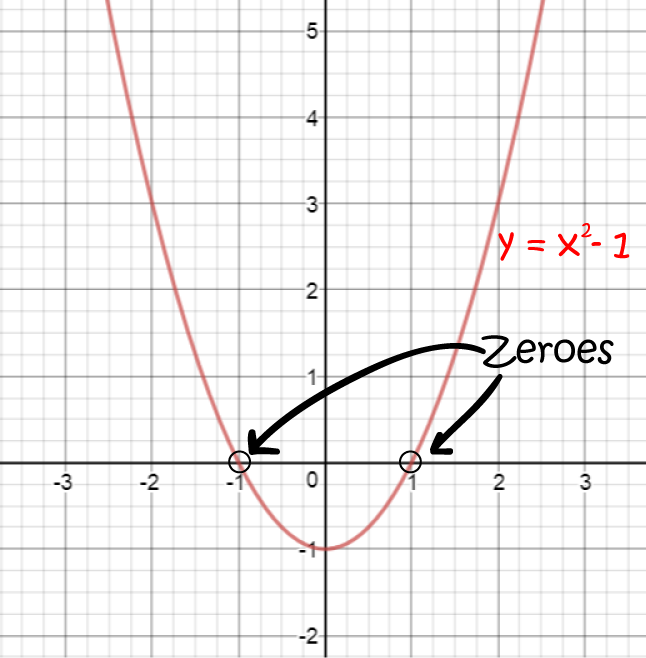
A zero of a function \(f(x) \) is a place where \(f(x) = 0\). In other words, it's a place where the graph of \(f(x)\) crosses the \(x\)-axis.
The function in the picture is \(f(x) = x^2 -1\). It crosses the \(x\)-axis at \(x = 1\) and \(x = -1\). So, it has zeroes at \(x = 1\) and \(x = -1\).
Many people call the zeroes of a function the "roots" of a function. They mean exactly the same thing.
Description
The aim of this dictionary is to provide definitions to common mathematical terms. Students learn a new math skill every week at school, sometimes just before they start a new skill, if they want to look at what a specific term means, this is where this dictionary will become handy and a go-to guide for a student.
Audience
Year 1 to Year 12 students
Learning Objectives
Learn common math terms starting with letter Z
Author: Subject Coach
Added on: 4th Dec 2017
You must be logged in as Student to ask a Question.
None just yet!