Year 10+ Constructions
Chapters
Constructing a Square of a Given Side Length
Constructing a Square of a Given Side Length
Compass and straight edge constructions are of interest to mathematicians, not only in the field of geometry, but also in algebra. For thousands of years, beginning with the Ancient Babylonians, mathematicians were interested in the problem of "squaring the circle" (drawing a square with the same area as a circle) using a straight edge and compass. This problem is equivalent to finding the area of a circle. It turns out that this is impossible, but no-one managed to prove this until 1882!
However, it is possible to construct a square of a given side length, just not a square of side length \(\sqrt{\pi}\). This is because \(\sqrt{\pi}\) is irrational, and any side we draw will have a rational length - it has to end at an exact point!
For this construction, you will need a straight edge (ruler - but you won't be measuring anything), a pair of compasses, a pencil and paper. I have drawn the pictures using the robocompass app. It's fun to play with, and you can use it to do all sorts of geometric constructions. There's a little bit of coding to learn, but a list of instructions is provided. Once you've written your little program, you can invite a few friends over to enjoy the beauty of the construction. Be warned that, when you are using it to draw arcs, the robocompass compass point may appear to be a little away from the centre, but the drawing is actually accurate.
The Construction

Step 1: Start with a line segment \(AB\). This will be the first side of your square. In the next five steps, we're going to construct a perpendicular to this line segment at the point \(B\).
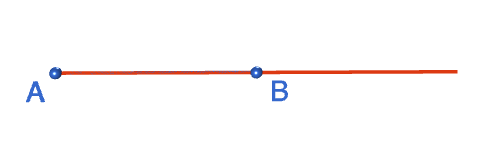
Step 2: Extend the line segment \(AB\) to the right. it doesn't matter how far, just give yourself enough room to construct the perpendicular.
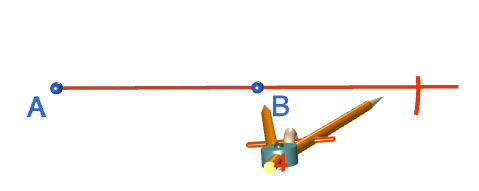
Step 3: Open the compasses out to a comfortable width. You're going to put arcs on either side of the point \(B\) that cut line segment \(AB\) and its extension, so make sure that your arcs will fit. With the compasses centred at \(B\), draw two arcs cutting the line segment on either side of \(B\). Label the points where these arcs cut the line segment with an \(E\) and an \(F\). Note: the robocompass point in the picture is slightly away from point \(B\). This is just a problem with the animation. Make sure the tip of your compasses is centred exactly at point \(B\).
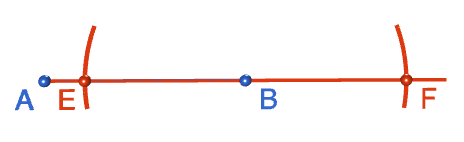
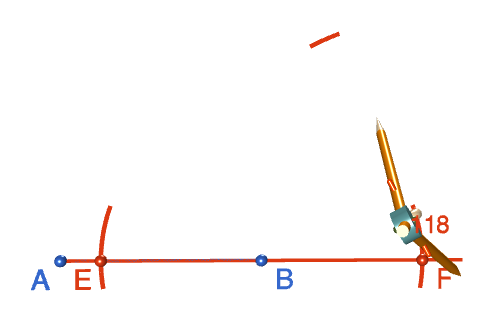
Step 4:Open out the compasses to any reasonably sized radius, and place the tip at point \(F\). Draw an arc above point \(B\). Make sure your tip is exactly on point \(F\).
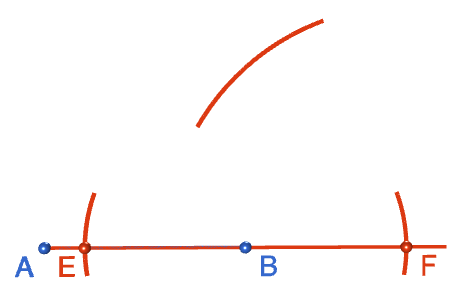
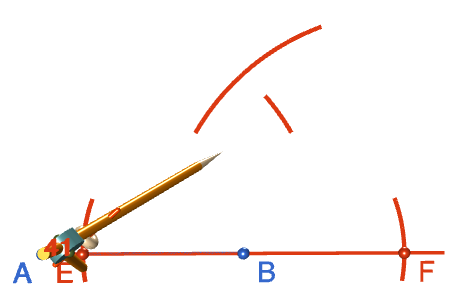
Step 5: Keeping the radius the same, move the tip of the compasses to point \(E\) and draw another arc above \(B\) that intersects with the arc you drew in step 4. Label the point where the arcs intersect with an \(H\). Note: the robocompass point in the picture is slightly away from point \(E\). This is just a problem with the animation. Make sure the tip of your compasses is centred exactly at point \(E\).
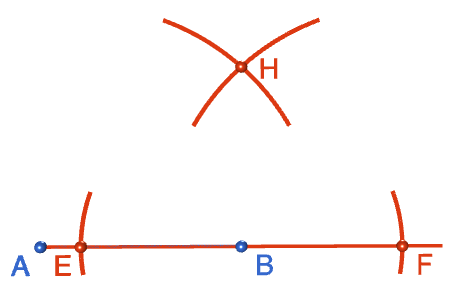
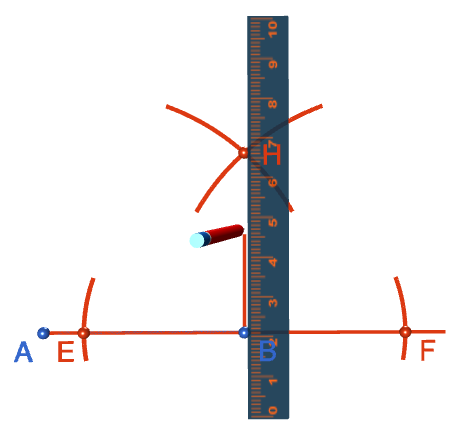
Step 6: Now it's time to draw the line segment that will form the second side of your square. Draw a line from \(B\), through \(H\) and beyond, using your straight edge. This line will be at right angles to the side \(AB\).
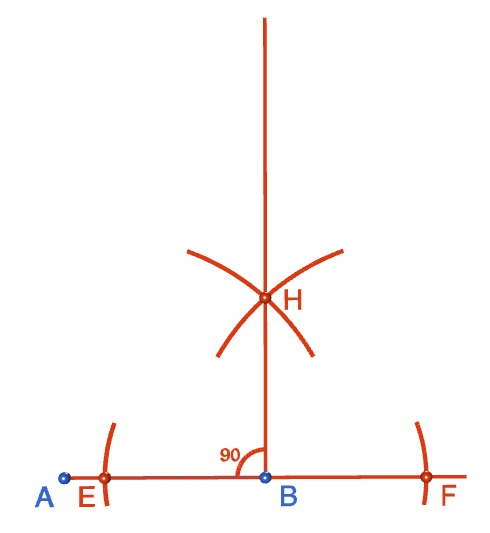
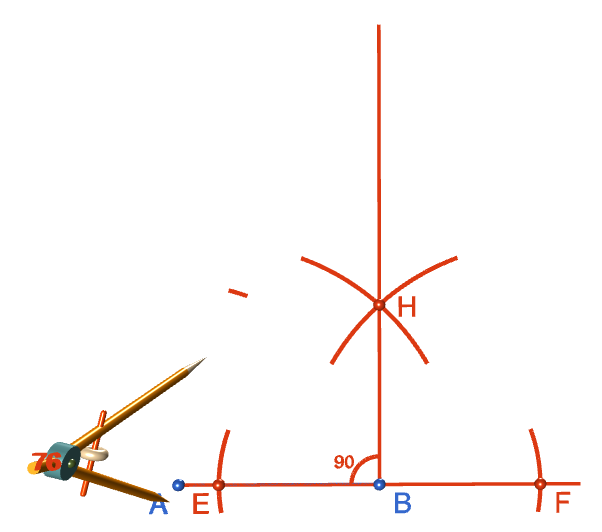
Step 7: We're now going to construct the other three sides of the square. Place the tip of your compasses exactly on point \(A\) and open them out to a radius that matches the length of line segment \(AB\). Keep this radius fixed for the rest of the construction. Draw an arc directly above the point \(A\).

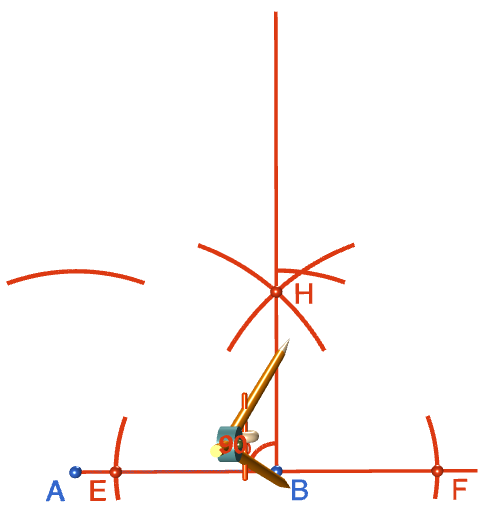
Step 8: Keeping the same radius as in step 7, move the tip of the compasses to point \(B\) and draw an arc intersecting the line segment you constructed in steps 2 to 6. Label the point where this arc intersects with the line segment with a \(C\). This is the third vertex of your square.
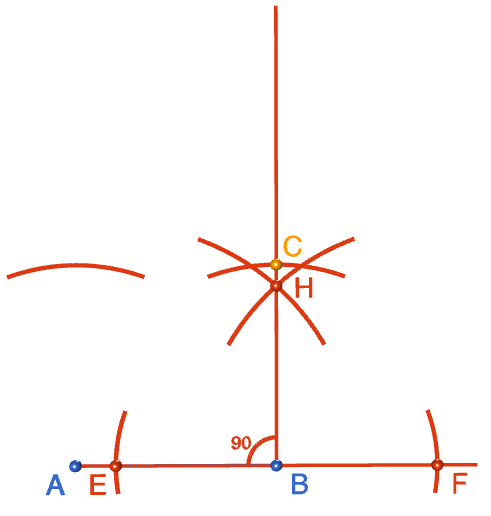
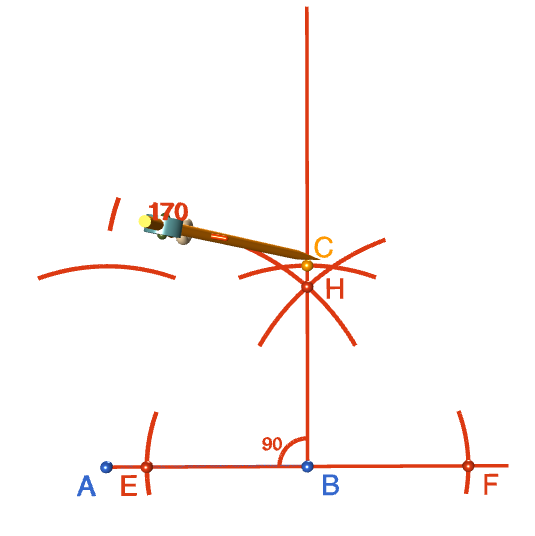
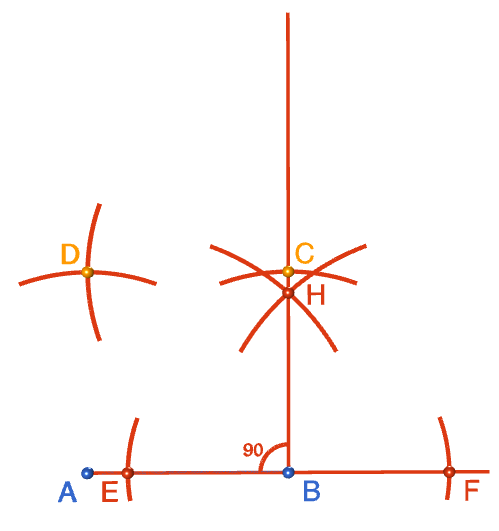
Step 9: Keeping the same radius as in step 8, move the tip of the compasses to point \(C\) and draw an arc intersecting the arc above \(A\). Label the point of intersection of the two arcs with a \(D\). This is the fourth vertex of your square.
Description
This tutorial will expose you to Rulers and how to use them. We will also have a close look as set square and compass constructions. Your feedback is important to us, if you like any other topic covered under this tutorial, please do let us know.
Audience
Year 10 or higher
Learning Objectives
Ruler and compass constructions and more
Author: Subject Coach
Added on: 27th Sep 2018
You must be logged in as Student to ask a Question.
None just yet!