Dihedral Angle

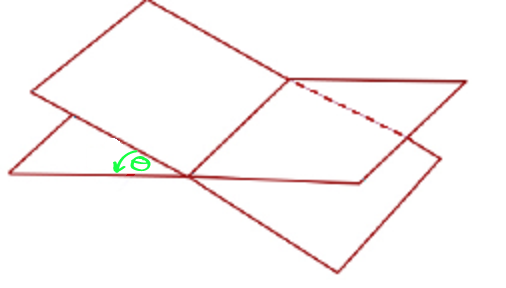
A dihedral angle is an angle between two planes that intersect. When we find a dihedral angle, we are really finding the angle between the lines that are perpendicular to each plane. To find the dihedral angle we need:

1. Cartesian equations \(A_1 x + B_1 y + C_1 z + D_1 = 0\) and \(A_2 x + B_2 y + C_2 z + D_2 = 0\) for the two planes.
2. The formula:
   \( \cos \theta = \dfrac{A_1A_2 + B_1 B_2 + C_1 C_2}{\sqrt{A_1^2 + B_1^2 + C_1^2}\sqrt{A_2^2 + B_2^2 + C_2^2}} \)

Once we've calculated the cosine of \(\theta\), we can find \(\theta\) using the inverse cosine function.

Note: For those who know about these things, we calculate the cosine of the dihedral angle by taking the dot product of two normal vectors to the planes, and dividing by their lengths. For those who don't know about these things: forget you ever read the preceding sentence.

Let's find the angles between a couple of planes.

Example 1

Find the dihedral angle between the planes \(x + 2y - 4z + 6 = 0\) and \(x + 2y + 3z - 4 = 0\).

Solution:

Using the formula yields:

Example 2

Find the dihedral angle between the planes \(2x - y + z - 2 = 0\) and \(x + y + 4 = 0\).

Solution:

Using the formula yields: