Year 10+ Lines and Angles
Chapters
Radians
Radians
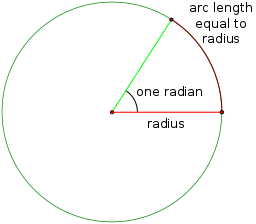
As you start to do more complicated mathematics, you will be introduced to the radian as a unit for measuring angles. A radian is the angle formed at the centre of a circle
by an arc with the same length as the radius of the circle. Mathematicians like radians for a number of reasons:
- It is a measurement based on the radius of the circle. Degrees really have nothing to do with the circle.
- As \(x\) gets close to zero, \(\sin (x)\) and \(\tan (x)\) get close to \(x\).
- Calculus works much more nicely with radians than with degrees. We don't have to multiply by pesky constants.
What Does One Radian Look Like?
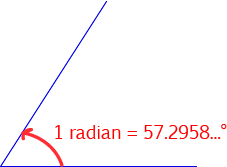
So that you can see what one radian looks like, here's an angle that measures 1 radian. 1 radian works out to be \(57.2958\dots^\circ\).
Why Such a Funny Number?
Remember that one radian is the angle at the centre of a circle formed by an arc that has the same length as the radius of a circle? Well, the circumference of a circle is given by \(2\pi\) times its radius. So, a full revolution is equal to \(2\pi \text{ radians}\). In other words, \(360^\circ = 2 \pi \text{ radians}\), and so \(1 \text{ radian} = \dfrac{360}{2\pi} = \dfrac{180}{\pi}^\circ = 57.2958\dots^\circ\).
Since there are \(2\pi\) radians in a whole circle, there are \(\pi \text{ radians}\) in a semicircle. This tells us that \(\pi \text{ radians} = 180^\circ\), as shown in the picture below

The Sizes of Some other Common Angles
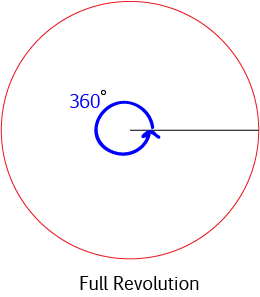
A full turn (a full revolution) is \(360^\circ\). This is also the angle at the centre of a whole circle. So, a full turn is equal to \(2\pi \text{ radians}\).
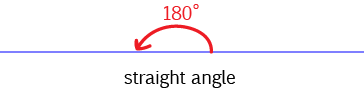
A straight angle (a half turn) is \(180^\circ\). This is the angle at the centre of a semicircle, so a straight angle is equal to \(\pi \text{ radians}\).
A right angle (also known as a quarter turn) is \(90^\circ\). This is also the angle at the centre of a quarter circle, so a right angle is equal to \(\dfrac{\pi}{2} \text{ radians}\).
In general, to convert from radians to degrees we multiply the angle in radians by \(180^\circ\) and divide it by \(\pi\).
To convert from degrees to radians, we multiply the angle in degrees by \(\pi\) and divide it by \(180\).
The table below gives a list of some common angles in degrees, and their equivalents in radians.
| Degrees | Radians (exact) | Radians (approximate) |
|---|---|---|
| \(0^\circ\) | \(0\) | \(0\) |
| \(30^\circ\) | \(\dfrac{\pi}{6}\) | \(0.524\) |
| \(45^\circ\) | \(\dfrac{\pi}{4}\) | \(0.785\) |
| \(60^\circ\) | \(\dfrac{\pi}{3}\) | \(1.047\) |
| \(90^\circ\) | \(\dfrac{\pi}{2}\) | \(1.571\) |
| \(120^\circ\) | \(\dfrac{2\pi}{3}\) | \(2.094\) |
| \(135^\circ\) | \(\dfrac{3\pi}{4}\) | \(2.356\) |
| \(150^\circ\) | \(\dfrac{5\pi}{6}\) | \(2.618\) |
| \(180^\circ\) | \(\pi\) | \(3.142\) |
| \(270^\circ\) | \(\dfrac{3\pi}{2}\) | \(4.712\) |
| \(360^\circ\) | \(2\pi\) | \(6.283\) |
Conclusion
I know you're probably feeling worried about using this complicated unit called radians at present. It's something new to get used to, and it's hard to visualise what a radian is. However, do persevere and get used to radians. They are much better for doing mathematics. Try, at least, to remember how to convert from degrees to radians and back again. If all the angles in a question are in radians, you really need to give your answer in radians. If the angles in the question are in degrees, you need to give your answer in degrees. When you're doing calculus, angles will always be measured in radians. Radians really do make the mathematics work more easily.
Description
In this mini book, you will learn about
- Alternate angles
- Cointerior angles
- Radians
- Vertically Opposite Angles
and several other topics related to lines and angles.
Audience
Year 10 or higher
Learning Objectives
To learn the basics of Lines and Angles stream of Geometry
Author: Subject Coach
Added on: 28th Sep 2018
You must be logged in as Student to ask a Question.
None just yet!