Cubes

Many things, like 6-sided dice, sugar cubes and Rubik's cubes are shaped like cubes. They are chosen for the most commonly used dice because every face has the same shape and size.

Cubes also occur naturally as the crystal form for many minerals because the atoms join together as the corners of a cube. For example, salt (left) and iron pyrite (right) naturally form crystals in the shape of cubes. We call objects that are shaped like cones cubic. So, what exactly is a cube, and what are its properties?

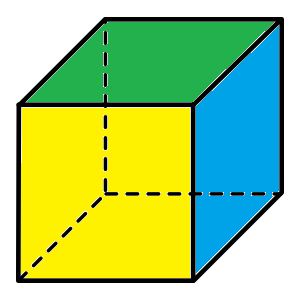
The Properties of a Cube

Cubes are solids with a six flat faces. Each flat face has the same size and shape: it has four edges, four right-angled corners, and is shaped like a square.

A cube has 12 edges and 8 vertices (corner points). Three edges meet at each vertex.

Another name for a cube is a hexahedron: cubes are polyhedra (solids with flat faces) with six (hexa-) sides.

Cubes are one of the \(5\) Platonic solids.

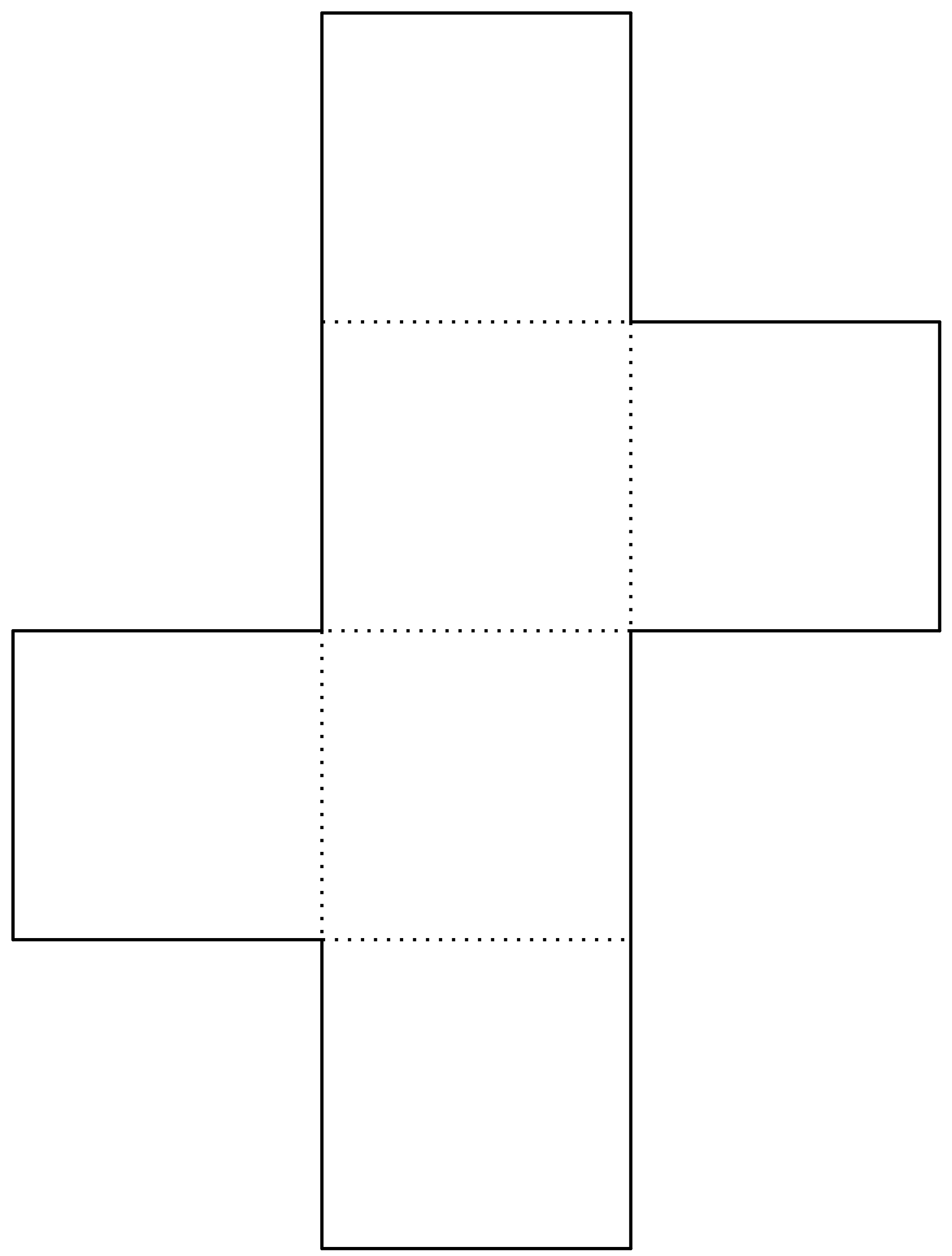
Building a Cube

You can make a cube yourself by printing the following net (template), cutting it out along the solid lines, folding it along the dotted lines and taping the edges together.

Finding the Surface Area and Volume of a Cube

Because a cube is a regular polyhedron, every edge of the cube has the same length.

Finding the Surface Area of a Cube

The cube has \(6\) sides, each of which is shaped like a square. As the area of a square is equal to the square of its side length,

For example, the surface area of a cube with edge length \(3\) cm is

Finding the Volume of a Cube

The cube is a rectangular prism in which all three of the length, width and height are equal. So, its volume is given by

For example, the volume of a cube with edge length \(3\) cm is