Year 10+ 3D Geometry
Chapters
Cylinders
Cylinders

You see cylinders every day. Many things, like toilet paper, cotton reels and tin cans are shaped like cylinders. We use the word cylindrical to describe things that are shaped like
cylinders. Just about anything that you roll up, like baking paper, paper towels, foil or cling wrap will be rolled up on a cylindrical tube. This is the easiest shape to use to roll things up on or unroll things from.
Many cakes, like this yummy chocolate cake, also have a cylindrical shape. All those years ago, when someone came up with the revolutionary idea of a wheel, they realised that cylinders
were an ideal shape to use to roll things along. So, what exactly is a cylinder, and what are its properties?


The Properties of a Cylinder
A cylinder is a solid with one curved surface and two flat faces (the base and the top). The flat faces are usually shaped like circles, and both have the same size.
Every cross section of the cylinder, parallel to the base, has the same size and shape, but the cylinder is not a prism because it has a curved surface.
The cylinder is also not a polyhedron because it has a curved surface. Polyhedrons only have flat surfaces.

Building a Cylinder
You can make a cylinder yourself by printing the following net (template), cutting it out along the solid lines, folding it, rolling the rectangle around the two circles,
and taping the edges together.

Finding the Surface Area of a Cylinder

The surface area of a cylinder may be split up into two parts:
- The areas of the base and top. For a circular cylinder, this is \(2 \pi r^2\) (twice the area of a circle, because there are two), where \(r\) is the radius of the cylinder.
- The area of the curved surface. This is equal to \(2 \pi r h\), where \(r\) is the radius of the cylinder, and \(h\) is the height of the cylinder, as shown in the picture on the left.
For example, if we were asked to find the surface area of a cylinder with height \(h = 3\) cm and radius \(r = 4\) cm, then we would calculate:
Finding the Volume of a Cone
The formula for the volume of a circular cylinder is
For example, the volume of a cylinder with height \(h = 3\) cm and base radius \(r = 4\) cm is given by
Volumes of Cones and Volumes of Cylinders
Did you notice something familiar about the formula for the volume of a cylinder? It looks a lot like the formula for the volume of a cone.
In fact, we can draw a cone of the same base radius and height inside a cylinder, as shown in the picture below:
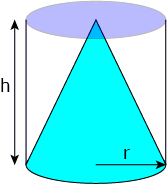
If \(\dfrac{1}{3}\) is sounding awfully familiar to you, that's because the volume of a right pyramid is also equal to \(\dfrac{1}{3}\) of the volume of the prism of the same base and height.
Cylinders with Differently Shaped Bases
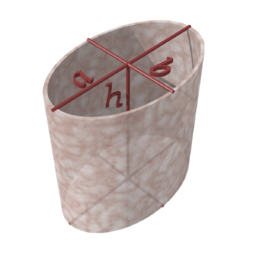
Cylinders can also have ellipses as their bases. We would then have to modify the formulas for the surface area and volume of the cylinder to include the area and perimeter of an ellipse, rather than the area and circumference of a circle. Read the articles on the perimeter and area of ellipses to find out how.
Description
There are several lessons related to 3D geometry such as
- Euler's formula
- Vertices, Edges and Faces
- Volumes of 3D shapes
- etc
Even though we've titled this lesson series to be more inclined for Year 10 or higher students, however, these lessons can be read and utilized by lower grades students.
Prerequisites
Understanding of 3D shapes
Audience
Year 10 or higher, but suitable for Year 8+ students
Learning Objectives
Get to know 3D Geometry
Author: Subject Coach
Added on: 27th Sep 2018
You must be logged in as Student to ask a Question.
None just yet!