Prisms

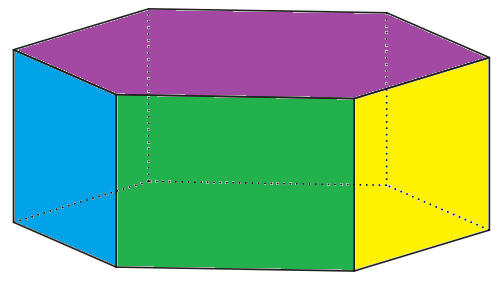
Prisms are 3-dimensional (solid) objects with

• 2 bases (ends) that are congruent (identical) and parallel to each other
• All faces flat
• All edges straight
• Cross-sections parallel to the base that are always congruent to the bases.

The bases of a prism are parallel to each other:

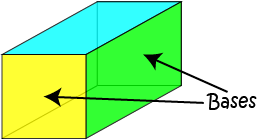
A cross-section is a view of an object formed by taking a slice through it. In geometry, a cross-section is the shape formed when we cut through a 3-dimensional object with a plane.

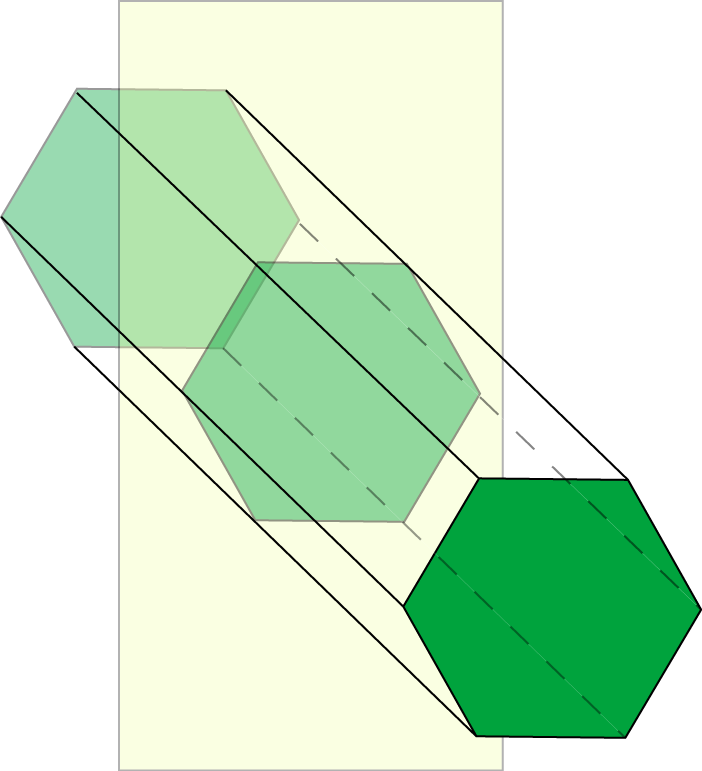
For example, the cross-sections of this hexagonal prism, parallel to the base are all hexagons

The sides of a prism are always parallelograms (4-sided plane shapes with two pairs of parallel sides).

Right and Oblique Prisms

The sides of a right prism are at right angles to the base. They are always rectangles.

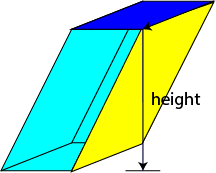
However, it is possible for a prism to have sides that are not at right angles to the base. Then we say that the prism is oblique, and its sides are parallelograms. The bases of an oblique prism are not directly above each other. Oblique prisms lean to the side like the one in this picture.

Regular and Irregular Prisms

Prisms are regular if their bases are regular polygons (flat shapes with straight edges, all of which have the same length).

However, the bases of prisms do not need to be regular polygons. The prism in the picture has its bases shaped like trapeziums. Trapeziums are irregular quadrilaterals, so this prism is irregular.

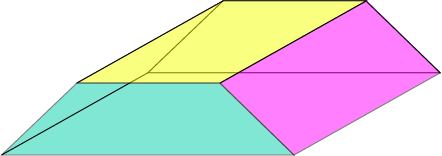
Examples of Prisms and Their Cross-Sections

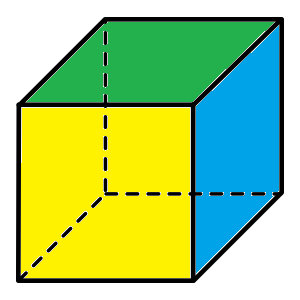
A cube is a square prism. The cross-sections of a cube parallel to its bases (pick any face) are squares.

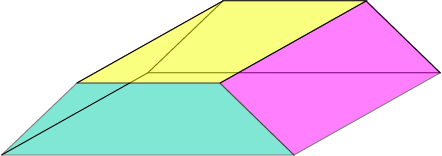
Although its bases are trapeziums, this solid is a prism. The cross-sections parallel to its bases are trapeziums.

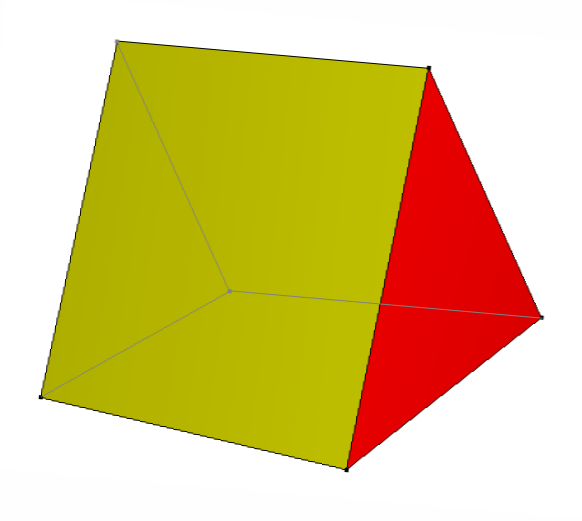
Like all prisms, the cross-sections of this triangular prism, parallel to the base, all have the same size and shape as its base. They are all triangles.

Surface Area of a Prism

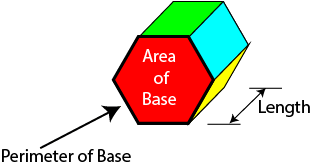
The Surface Area of a Prism is given by the following formula:

\(\text{Surface Area} = 2 \times \text{Area of Base} + \text{Length} \times \text{Perimeter of Base}\)

Example

Find the surface area of a prism with base area \(40 \text{ m}^2\), base perimeter \(28 \text{ m}\) and length \(5 \text{ m}\).

Solution:

Volume of a Prism

The Volume of a Prism is given by the following formula:

\(\text{Volume} = \text{Area of Base} \times \text{Length} \)

Example

Find the volume of a prism with base area \(40 \text{ m}^2\) and length \(5 \text{ m}\).

Solution: