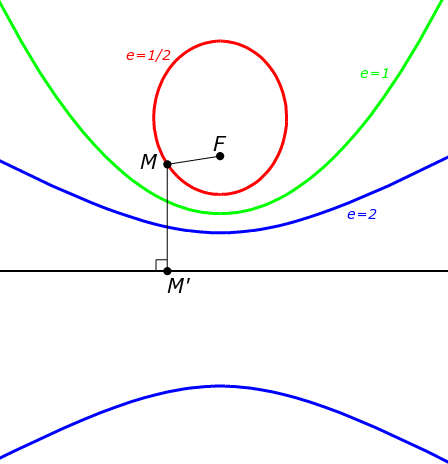
The eccentricity of a conic section (a circle, an ellipse, a parabola or a hyperbola) tells us how different from a circle it is.

Circles have eccentricity zero, but as the conic section opens out and its curves become less like those of a circle, its eccentricity increases.

We use \(e\) as notation for the eccentricity of a conic section. This, of course, is a completely different \(e\) from Euler's constant, which has the fixed value \(2.71828\dots\).

Different types of conic sections have different eccentricities:

• All circles have \(e=0\)
• The eccentricity of ellipses varies: \(0 .
• All parabolas have \(e = 1\).
• Hyperbolas all have \(e > 1\).
• Being as uncurved as you can get, straight lines have infinite eccentricity.

Regardless of its radius, the eccentricity of a circle is always zero. That's not too hard to calculate, is it?

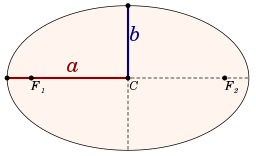
You have to do a bit of work to find the eccentricity of an ellipse. It's given by the formula

Notice you get \(0\) if \(a = b\). Then the ellipse is a circle.

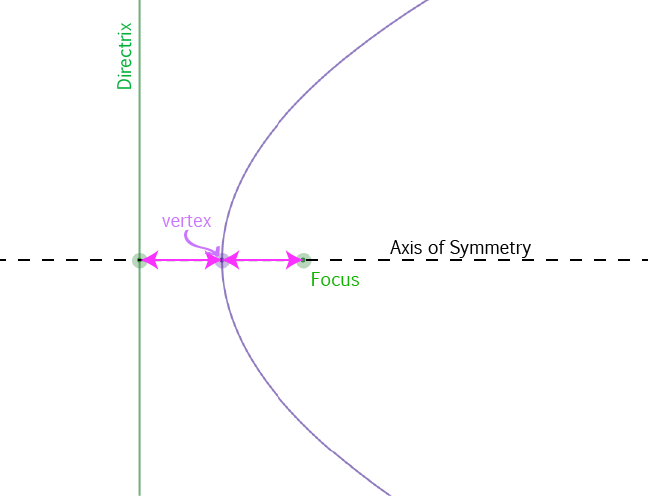
The second easiest conic section to calculate the eccentricity for is the parabola. Its eccentricity is always 1. (What? 1 is simpler than 0, isn't it?)

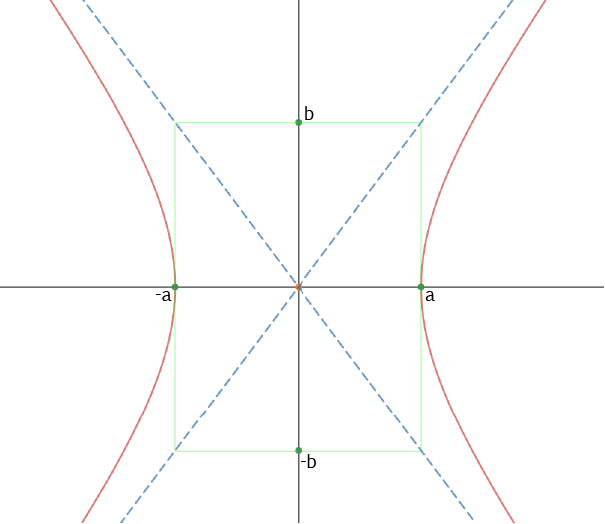
Finding the eccentricity of a hyperbola is a little trickier than the others. The equation of a hyperbola should look something like this:

Then the eccentricity of the hyperbola is given by the formula: There's another formula relating the eccentricity of the hyperbola to the focal length and the distance of each vertex from the centre of the hyperbola (the point where its asymptotes cross), but we'll talk about that in the article on the hyperbola.