Year 10+ Plane Geometry
Chapters
Theorems About Similar Triangles
Theorems About Similar Triangles
The Triangle Proportionality Theorem
This theorem states that if \(ADE\) is a triangle, and \(BC\) is drawn parallel to the side \(DE\), then \(\dfrac{AB}{BD} = \dfrac{AC}{CE}\).

Proof: To prove this theorem (show it is true), we add an extra line \(BF\) parallel to \(AE\) to form parallelogram \(BCEF\) as shown in the diagram below:
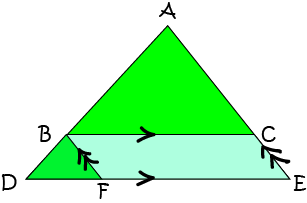
Next, we show that triangles \(ABC\) and \(BDF\) are similar:
- \(\angle ABC = \angle BDF\) as they are corresponding angles.
- \(\angle BFD = \angle ACB\) as they are alternate (interior) angles.
We use corresponding sides of similar triangles \(ABC\) and \(BDF\) to establish the result:
- Sides \(AB\) and \(BD\), and sides \(AC\) and \(BF\) are corresponding sides.
- Since the triangles are similar, \(\dfrac{AB}{BD} = \dfrac{AC}{BF}\).
- \(BF = CE\) (opposite sides of parallelogram \(BCEF\)).
- So, \(\dfrac{AB}{BD} = \dfrac{AC}{CE}\), establishing our result.
Example 1
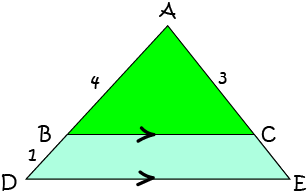
Find the length of \(CE\).
Solution:
By the Triangle Proportionality Theorem, \(\dfrac{AB}{BD} = \dfrac{AC}{CE}\). So,
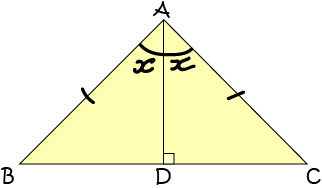
The Angle Bisector Theorem
This theorem states that if \(ABC\) is a triangle, and \(AD\) is drawn so that it bisects \(\angle BAC\), then \(\dfrac{AB}{BD} = \dfrac{AC}{DC}\).
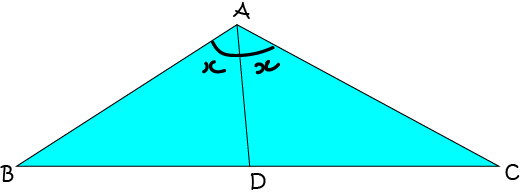
Proof: To prove this theorem (show it is true), we label the triangle as as shown in the diagram below:
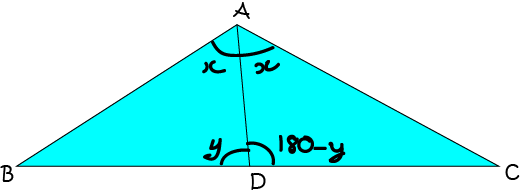
Then
Using the Sine Law on \(\triangle ACD\) gives
The result follows since \(\sin (180 - y)^\circ = \sin y^\circ\). Therefore,
An interesting consequence of this result is that if \(\triangle ABC\) is isosceles, then triangles \(ABD\) and \(ACD\) are congruent.
Example 2
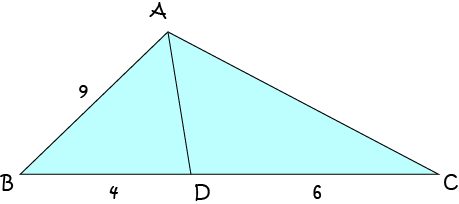
Find the length of \(AC\).
Solution:
By the Angle Bisector Theorem, \(\dfrac{AB}{BD} = \dfrac{AC}{DC}\). So,
Areas of Similar Triangles
If triangles \(ABC\) and \(XYZ\) are similar and have sides in the ratio \(p:q\), then their areas are in the ratio \(p^2:q^2\)
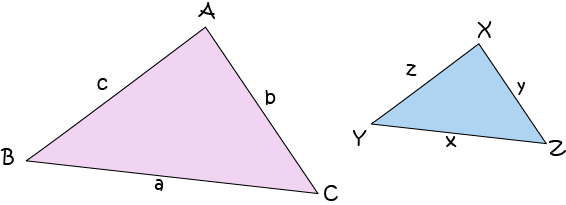
Proof
Suppose triangles \(ABC\) and \(XYZ\) are similar and have sides in the ratio \(p:q\). Then we can use the general formula for the area of a triangle to find
- \(\text{Area}_{ABC} = \dfrac{1}{2}\;bc \sin A\)
- \(\text{Area}_{XYZ} = \dfrac{1}{2}\;yz \sin X\)
\(\dfrac{y}{b} = dfrac{p}{q}\) and \(\dfrac{z}{c} = dfrac{p}{q}\).
So, \(y = \dfrac{bp}{q}\) and \(z = \dfrac{cp}{q}\).
We also have \(A = X\) since the triangles are similar.
So, we can calculate
Example 3
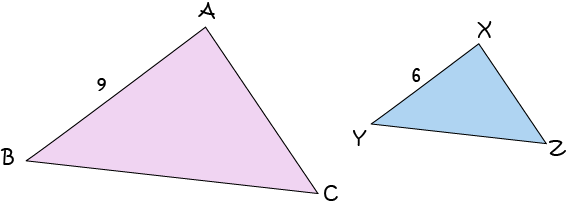
The area of triangle \(ABC\) is \(60 \text{ cm}^2\). If triangles \(ABC\) and \(XYZ\) are similar, what is the area of triangle \(XYZ\)?
Solution:
The two triangles are similar, with corresponding sides in the ratio \(6: 9\), so their areas are in the ratio \(6^2:9^2 = 36:81 = 4:9\). Therefore, the area of triangle \(XYZ\) is equal to
Description
In these chapters you will learn about plane geometry topics such as
- Area (Irregular polygons, plane shapes etc)
- Perimeter
- Conic sections (Circle, Ellipse, Hyperbola etc)
- Polygons (Congruent, polygons, similar, triangles etc)
- Transformations and symmetry (Reflection, symmetry, transformations etc)
etc
Even though these chapters are marked for Year 10 or higher students, several topics are for students in Year 8 or higher
Audience
Year 10 or higher, suitable for Year 8 + students as well.
Learning Objectives
Learn about Plane Geometry
Author: Subject Coach
Added on: 28th Sep 2018
You must be logged in as Student to ask a Question.
None just yet!