Implicit Differentation

Introduction

Sometimes functions are explicit about their definitions:

tells you pretty blatantly that to turn an \(x\) into an \(f(x)\), you have to square the \(x\) and multiply it by \(3\).

Other functions are a little more coy about how you evaluate them. For example, although

definitely gives you a relationship between \(x\) and \(y\), it isn't quite so easy to see what the value of \(y\) corresponding to a given value of \(x\) is. We call functions like this, implicitly defined functions. This article talks about how to differentiate them, using a technique that's, oddly enough, called implicit differentiation.

Let's start by thinking about a useful real world problem that you probably won't find in your maths textbook.

Alice the cow is a bit of a pig. She's decided to see how quickly she can guzzle grass from Farmer Hogg's field.

Alice has worked out that the amount of grass she can guzzle at time \(t\) minutes is determined by the implicitly defined formula

\(x^2t + 2tx = 19\),

and wants to find her rate of grass consumption after \(t = 3 \text{ minutes}\).

To find this rate, Alice will need to differentiate her function. But there's a problem: the function is defined implicitly, and standard differentiation techniques won't work. Let's find out how Alice can differentiate her function. We'll start out with some other examples, and come back to Alice later.

How Do We Implicitly Differentiate?

1. Differentiate both sides of the equation with respect to \(x\). Remember: \(y\) is a function of \(x\), and its derivative is \(\dfrac{dy}{dx}\).
2. Pull all the \(\dfrac{dy}{dx}\)s onto one side of the equation (doesn't matter which).
3. Solve for \(\dfrac{dy}{dx}\).

Example:

Find \(\dfrac{dy}{dx}\) if \(x^3 + \sin(y) = 17\).

Walk along the equation, differentiating as you go, remembering that \(y\) is a function of \(x\), and its derivative is \(\dfrac{dy}{dx}\):

Now find each derivative:

• \(\dfrac{d}{dx} (x^3) = 3x^2 \) by the Power Rule.
• \(\dfrac{d}{dx}(\sin (y)) = \cos(y)\;\dfrac{dy}{dx}\) by the Chain Rule (see the explanation below).
• \(\dfrac{d}{dx}(17) = 0\) as \(17\) is a constant.

Stitching this together gives: Pull all the \(\dfrac{dy}{dx}\)s onto one side: and solve for \(\dfrac{dy}{dx}\):

Using the Chain Rule to Differentiate Functions of \(y\)

One thing you absolutely have to remember is that \(y\) is a function of \(x\), with derivative \(\dfrac{dy}{dx}\), so you need to use the chain rule to differentiate functions of \(y\).

Let's work through how \(\sin(y)\) becomes \(\cos(y)\;\dfrac{dy}{dx}\) in the above example.

We'll start by recalling the chain rule using Leibniz's notation:

Now plug in \(u = \sin(y)\): So,

To oversimplify things (but it works): differentiate with respect to \(y\), and multiply the result by \(\dfrac{dy}{dx}\).

Another Example

Sometimes we need to use the product rule when we're differentiating implicitly. Let's try differentiating the function

Walk along the equation, differentiating as you go, remembering that \(y\) is a function of \(x\), and its derivative is \(\dfrac{dy}{dx}\):

To find \(\dfrac{d}{dx}(x^4 y)\), we'll need to use the product rule (have a look at the article on the product rule if you don't remember how this works) Now stitch it all together: Now, pull \(\dfrac{dy}{dx}\) to one side: Finally, solve for \(\dfrac{dy}{dx}\):

Now we know enough to help Alice.

Let's Solve Alice's Problem

Remember, Alice wants to know how quickly she can guzzle grass from Farmer Hogg's field. Her grass consumption at time \(t\) is given by the equation \(x^2 t + 2tx = 19\), and Alice wants to know how quickly she'll be guzzling grass after \(t = 3\) minutes. This looks like a job for implicit differentiation.

Walk along the equation, differentiating as you go, remembering that \(x\) is a function of \(t\), and its derivative is \(\dfrac{dx}{dt}\):

To find \(\dfrac{d}{dt}(x^2 t)\) and \(\dfrac{d}{dt}(tx)\), we'll need to use the product rule (have a look at the article on the product rule if you don't remember how this works) Now stitch it all together: Now, pull all the \(\dfrac{dx}{dt}\)s to one side: Finally, solve for \(\dfrac{dx}{dt}\): Now, when \(t = 3\), Alice's function definition becomes \(9x^2 + 6x -19 = 0\), which is a quadratic, with roots \(x \approx 1.71\) and \(x \approx -3.71\). We don't want to think about Alice consuming negative grass, so we'll go with \(x \approx 1.71\) and evaluate our derivative: So, it looks like Alice is slowing down after 3 minutes. Her eyes are definitely too big for her tummy!

Another application of the derivative

Example

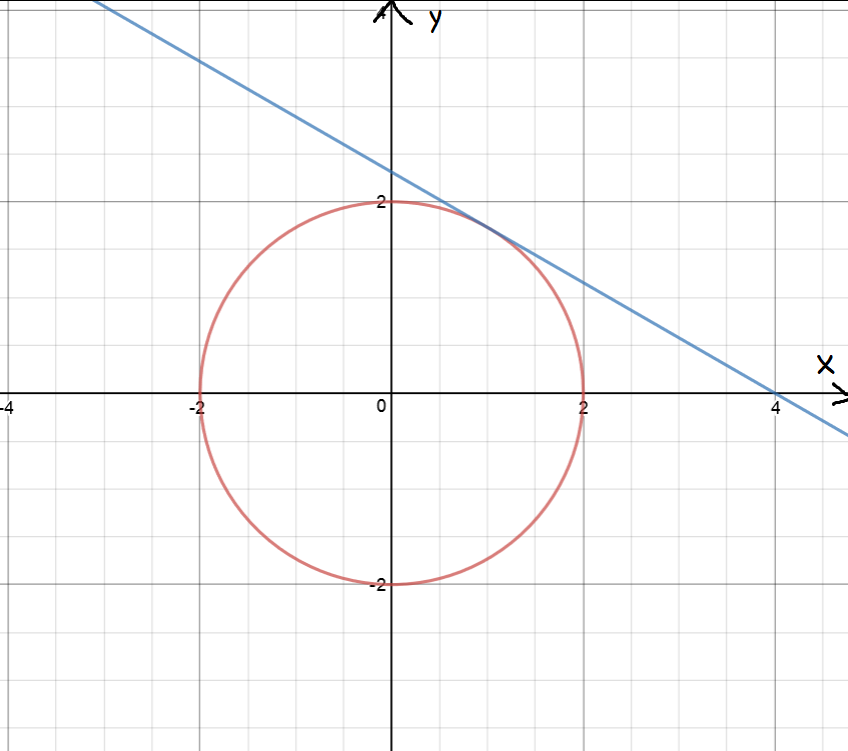
What is the slope of the tangent to the circle, \(x^2 + y^2 = 4 \) at the point \((1,\sqrt{3})\)?

We need to find \(\dfrac{dy}{dx}\). Start by differentiating implicitly:

\( \begin{align*} \dfrac{d}{dx}(x^2) + \dfrac{d}{dx}(y^2) &= \dfrac{d}{dx}(4)\\ 2x + 2y \;\dfrac{dy}{dx} &= 0\\ 2x &= - 2y \;\dfrac{dy}{dx}\\ \dfrac{dy}{dx} &= -\dfrac{2x}{2y}\\ &= -\dfrac{x}{y}. \end{align*} \)

Now substitute our point into the equation for the derivative to yield:

\( \begin{align*} \dfrac{dy}{dx} = -\dfrac{1}{\sqrt{3}}. \end{align*} \)

Now, plug the point \((1,\sqrt{3})\) into the equation \(y = -\dfrac{1}{\sqrt{3}} \;x + b\) to find \(b = \dfrac{4}{\sqrt{3}}\).

So, the equation of the tangent line is \(y = -\dfrac{1}{\sqrt{3}}\;x + \dfrac{4}{\sqrt{3}}\).

Using Implicit Differentiation to Differentiate Inverse Functions

We follow the following steps:

1. Start with the inverse function in explicit form, e.g. \(y = \cos^{-1}(x)\)
2. Rewrite it in implicit form, e.g. \(x = \cos(y)\). In other words, get rid of the inverse function.
3. Differentiate implicitly (e.g. see below)
4. Solve for \(\dfrac{dy}{dx}\)
5. Simplify, if necessary.

Example:

Find the derivative of \(y = \cos^{-1}(x)\)

1. Start with \(y = \cos^{-1}(x)\)
2. Get rid of the inverse: \(x = \cos(y)\)
3. Differentiate implicitly:
   \(\begin{align*} \dfrac{d}{dx}(x) &= \dfrac{d}{dx}(\cos(y))\\ 1 &= -\sin(y)\; \dfrac{dy}{dx} \text{ by the chain rule}\\ \end{align*} \)
4. Solve for \(\dfrac{dy}{dx}\): \(\dfrac{dy}{dx}= -\dfrac{1}{\sin(y)}\)

We can simplify this further, using \(\sin^2 y + \cos^2 y = 1\), which gives \(\sin(y)= \sqrt{1 - \cos^2 y} = \sqrt{1 - x^2}\).

Plugging this in gives:

\( \dfrac{dy}{dx} = - \dfrac{1}{\sqrt{1 - x^2}},\)

which should look familiar from our rules of derivatives article.

One last example:

Example:

Find the derivative of \(y = \ln(x)\)

1. Start with \(y = \ln(x)\)
2. Get rid of the inverse: \(x = e^y\)
3. Differentiate implicitly: \(\begin{align*} \dfrac{d}{dx}(x) &= \dfrac{d}{dx}(e^y)\\ 1 &= e^{y}\; \dfrac{dy}{dx} \text{ by the chain rule}\\ \end{align*} \)
4. Solve for \(\dfrac{dy}{dx}\): \(\dfrac{dy}{dx}= \dfrac{1}{e^y} = \dfrac{1}{x},\)

which should also be very familiar from our rules of derivatives article.

Things to Remember

To differentiate implicitly defined functions:

• Differentiate both sides of the equation with respect to \(x\). Remember: \(y\) is a function of \(x\), and its derivative is \(\dfrac{dy}{dx}\).
• Solve for \(\dfrac{dy}{dx}\).

To find the derivatives of inverse functions, rewrite \(x\) as a function of \(y\) and differentiate implicitly.