Calculus
Chapters
Points of Inflection
Points of Inflection
Introduction
Points of Inflection are points where a curve changes concavity: from concave up to concave down,
or vice versa. Just to make things confusing,
you might see them called Points of Inflexion in some books. Call them whichever you like... maybe
you think it's quicker to write 'point of inflexion'.
Of course, you could always write P.O.I for short - that takes even less energy.
Purely to be annoying, the above definition includes a couple of terms that you may not be familiar with. If
you're wondering
what on earth concave up and concave down, rest assured that you're not alone. Let's
draw some pictures so we can
get a better idea:
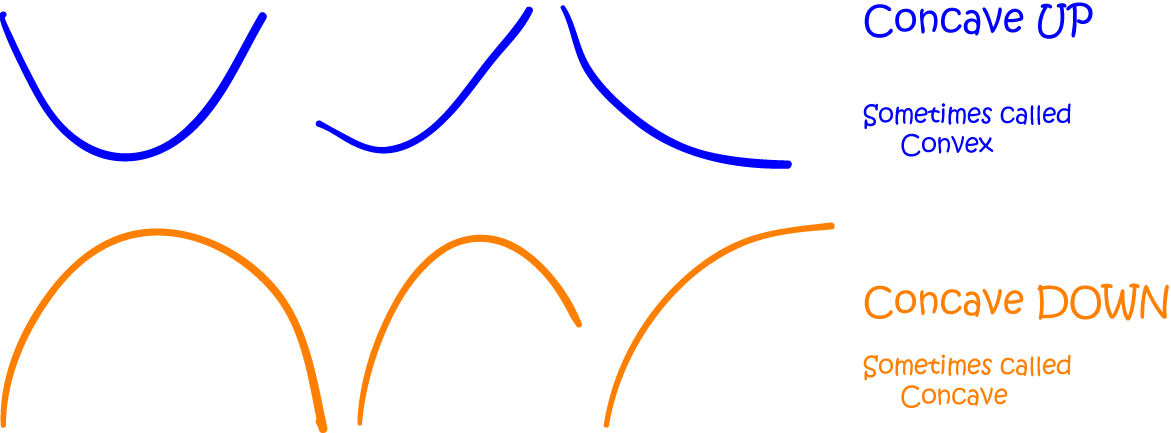
concave up when
its gradient increases as its values increase. I like to think of a parabola with the ends pointing
upwards
(one that's the 'right way up').
You might have written descriptions of concave up curves in Physics classes. They're the ones that are
'increasing at an
increasing rate' or 'decreasing at a decreasing rate'.
 ]
]
concave down when
its gradient decreases as its values increase. I like to think of a parabola with the ends pointing
downwards (one that's 'upside down').
You might have written descriptions of concave down curves in Physics classes. They're the ones that are
'increasing at a
decreasing rate' or 'decreasing at an increasing rate'.

The following pictures show some more curves that would be described as concave up or concave down:
Do you want to know more about concave up and concave down functions? The article on concavity goes into lots of gory details.
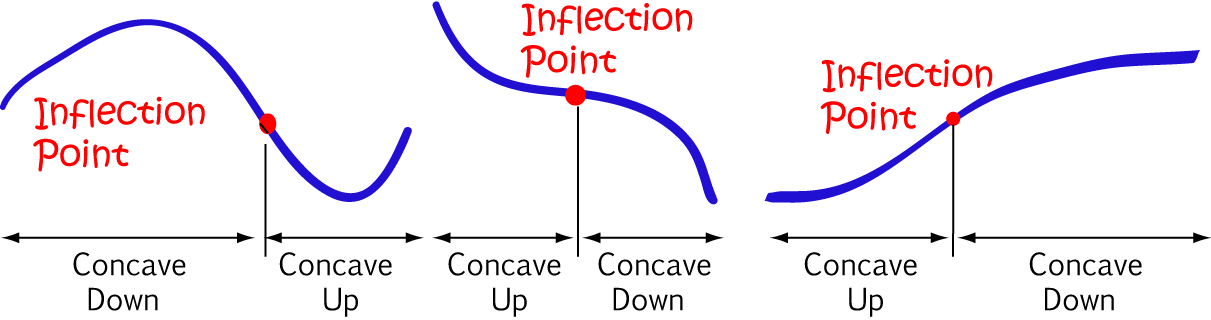
Finding Points of Inflection
To find a point of inflection, you need to work out where the function changes concavity. That is, where it changes from concave up to concave down or from concave down to concave up, just like in the pictures below.
Use Calculus
You guessed it! Calculus is the best tool we have available to help us find points of inflection. Derivatives
are what we need.
Remember, we can use the first derivative to find the slope of a function. However, we want to find out when the slope is increasing or decreasing, so we need to use the second derivative.
- If a function is concave up, then its second derivative is positive.
- If a function is concave down, then its second derivative is negative.
- What if the second derivative is zero? There might just be a point of inflection.
Note: You have to be careful when the second derivative is zero. Sometimes this can happen even if there's no point of inflection. For example, the second derivative of the function \(y = 17\) is always zero, but the graph of this function is just a horizontal line, which never changes concavity.
For there to be a point of inflection at \((x_0,y_0)\), the function has to change concavity from concave up to concave down (or vice versa) on either side of \((x_0,y_0)\).
Example

Find the points of inflection of \(y = 4x^3 + 3x^2 - 2x\).
Start by finding the second derivative:
- \(y' = 12x^2 + 6x - 2\)
- \(y'' = 24x + 6\)
Now, if there's a point of inflection, it will be a solution of \(y'' = 0\). In other words,
- For \(x
- For \(x > -\dfrac{1}{4}\), \(24x + 6 > 0\), so the function is concave up.
Quick Review of Derivatives
Just how did we find the derivative in the above example? There are a number of rules that you can follow to find derivatives. We used the power rule to find the derivatives of each part of the equation for \(y\), and then added them together
- The derivative of \(x^3\) is \(3x^2\), so the derivative of \(4x^3\) is \(4(3x^2) = 12x^2\)
- The derivative of \(x^2\) is \(2x\), so the derivative of \(3x^2\) is \(3(2x) = 6x\)
- Finally, the derivative of \(x\) is \(1\), so the derivative of \(-2x\) is \(-2(1) = -2\)
Adding them all together gives the derivative of \(y\): \(y' = 12x^2 + 6x - 2\).
Next, we differentiated the equation for \(y'\) to find the second derivative \(y'' = 24x + 6\).
Let's try one more example:
Example

Find the points of inflection of \(y = x^3 - 4x^2 + 6x - 4\).
Start by finding the second derivative:
- \(y' = 3x^2 - 8x + 6 \)
- \(y'' = 6x - 8\)
Now, if there's a point of inflection, it will be a solution of \(y'' = 0\). In other words,
- For \(x
- For \(x > \dfrac{4}{3}\), \(6x - 8 > 0\), so the function is concave up.
Description
Calculus is the branch of mathematics that deals with the finding and properties of derivatives and integrals of functions, by methods originally based on the summation of infinitesimal differences. The two main types are differential calculus and integral calculus.
Environment
It is considered a good practice to take notes and revise what you learnt and practice it.
Audience
Grade 9+ Students
Learning Objectives
Familiarize yourself with Calculus topics such as Limits, Functions, Differentiability etc
Author: Subject Coach
Added on: 23rd Nov 2017
You must be logged in as Student to ask a Question.
None just yet!