Homogeneous Differential Equations
Introduction
Differential Equations are equations involving a function and one or more of its derivatives.
For example, the differential equation below involves the function \(y\) and its first derivative \(\dfrac{dy}{dx}\).
Let's consider an important real-world problem that probably won't make it into your calculus text book:
 A plague of feral caterpillars has started to attack the cabbages in Gus the snail's garden. Gus observes that the cabbage leaves
are being eaten at the rate
A plague of feral caterpillars has started to attack the cabbages in Gus the snail's garden. Gus observes that the cabbage leaves
are being eaten at the rate
\( \dfrac{d \text{cabbage}}{dt} = \dfrac{\text{cabbage}}{t}\),
where \(t\) is the time in days after the initial infestation. He knows that \(6\) cabbage leaves were eaten
on the first day after the initial infestation,
and wants to know how many cabbage leaves will be eaten on the second day after
the infestation.
Gus has written down a
homogeneous differential equation. We'll find out what this means in a minute.
To work out how many cabbage leaves will be eaten on day \(2\), he needs to solve his differential equation and plug in \(t=2\). But how can he solve
the equation?
What are Homogeneous Differential Equations?
A first order differential equation is homogeneous if it can be written in the form:
\(
\dfrac{dy}{dx} = f(x,y),
\)
where the function \(f(x,y)\) satisfies the condition that \(f(kx,ky) = f(x,y)\) for all real constants
\(k\) and all \(x,y \in \mathbb{R}\). We will eventually solve homogeneous equations using separation of variables, but
we need to do some work to turn them into separable differential equations first. It might be useful to
look back at the article on separable differential equations before reading on. You can also read some more about Gus' battle against
the caterpillars there.
For example, the differential equation
\(\dfrac{dy}{dx} = \dfrac{x^2}{y^2},\)
where \(f(x,y) = \dfrac{x^2}{y^2}\) is a homogeneous differential equation. For any real number \(k\):
\(
f(kx,ky) = \dfrac{(kx)^2}{(ky)^2} = \dfrac{k^2 x^2}{k^2 y^2} = \dfrac{x^2}{y^2} = f(x,y).
\)
Solving Homogeneous Differential Equations
We need to transform these equations into separable differential equations. We begin by making the
substitution \(y = vx\). Differentiating gives
\( \dfrac{dy}{dx} = v\; \dfrac{dx}{dx} + x \; \dfrac{dv}{dx} = v + x \; \dfrac{dv}{dx}\)
by the product rule.
Let's see this in action on an example.
Example
Solve the differential equation \(\dfrac{dy}{dx} = \dfrac{y(x + y)}{xy} \)
First, check that it is homogeneous. Let \(k\) be a real number. Then
\(
\begin{align*}
\dfrac{ky(kx + ky)}{(kx)(ky)} = \dfrac{k^2(y(x + y))}{k^2 xy} = \dfrac{y(x + y)}{xy}.
\end{align*}
\)
So, it is homogenous.
Next, do the substitution \(y = vx\) and \(\dfrac{dy}{dx} = v + x \; \dfrac{dv}{dx}\):
\(\begin{align*}
v + x\;\dfrac{dv}{dx} &= \dfrac{xy + y^2}{xy}\\
&= \dfrac{x(vx) + (vx)^2}{x(vx)}\\
&= \dfrac{vx^2 + v^2 x^2 }{vx^2}\\
&= 1 + v
\end{align*}
\)
Rearranging gives
\(\begin{align*}
v + x \; \dfrac{dv}{dx} &= 1 + v\\
x\; \dfrac{dv}{dx} &= 1,
\end{align*}
\)
which is a separable differential equation!
Now, apply separation of variables:
Step 1: Separate the variables by moving all the terms in \(v\), including \(dv\),
to one side of the equation and all the terms in \(x\), including \(dx\), to the other.
\( dv = \dfrac{1}{x} \; dx\)
Step 2: Integrate both sides of the equation.
\(
\begin{align*}
\int \;dv &= \int \dfrac{1}{x} \; dx\\
v &= \ln (x) + C
\end{align*}
\)
Step 3: There's no need to simplify this equation.
Now substitute \(y = vx\), or \(v = \dfrac{y}{x}\) back into the equation:
\( \dfrac{y}{x} = \ln (x) + C\)
and multiply both sides by \(x\) to make \(y\) the subject of the equation:
\( y = x\ln (x) + Cx.\)
There, we've solved our first homogeneous differential equation!
Let's try another.
Example
Solve the differential equation \(\dfrac{dy}{dx} = \dfrac{x(x - y)}{x^2} \)
First, check that it is homogeneous. Let \(k\) be a real number. Then
\(
\begin{align*}
\dfrac{kx(kx - ky)}{(kx)^2} = \dfrac{k^2(x(x - y))}{k^2 x^2} = \dfrac{x(x - y)}{x^2}.
\end{align*}
\)
So, it is homogenous.
Next, do the substitution \(y = vx\) and \(\dfrac{dy}{dx} = v + x \; \dfrac{dv}{dx}\) to convert it into
a separable equation:
\(\begin{align*}
v + x\;\dfrac{dv}{dx} &= \dfrac{x^2 - xy}{x^2}\\
&= \dfrac{x^2 - x(vx)}{x^2}\\
&= \dfrac{x^2 - v x^2 }{x^2}\\
&= 1 - v
\end{align*}
\)
Rearranging gives
\(\begin{align*}
v + x \; \dfrac{dv}{dx} &= 1 - v\\
x\; \dfrac{dv}{dx} &= 1 - 2v,
\end{align*}
\)
which is a separable differential equation!
Now, apply separation of variables:
Step 1: Separate the variables by moving all the terms in \(v\), including \(dv\),
to one side of the equation and all the terms in \(x\), including \(dx\), to the other.
\( \dfrac{1}{1 - 2v}\;dv = \dfrac{1}{x} \; dx\)
Step 2: Integrate both sides of the equation.
\(
\begin{align*}
\int \dfrac{1}{1 - 2v}\;dv &= \int \dfrac{1}{x} \; dx\\
-\dfrac{1}{2} \ln (1 - 2v) &= \ln (x) + C
\end{align*}
\)
Step 3: Simplify this equation. First, write \(C = \ln(k)\), and then
take exponentials of both sides to get rid of the logs:
\(
\begin{align*}
-\dfrac{1}{2} \ln (1 - 2v) &= \ln (x) + \ln(k)\\
-\dfrac{1}{2} \ln (1 - 2v) &= \ln (kx)\\
\ln (1 - 2v)^{-\dfrac{1}{2}} &= \ln (kx)\\
(1 - 2v)^{-\dfrac{1}{2}} &= kx\\
\dfrac{1}{\sqrt{1 - 2v}} &= kx
\end{align*}
\)
Square both sides and take reciprocals:
\(
\begin{align*}
\dfrac{1}{1 - 2v} &= k^2x^2\\
1 - 2v &= \dfrac{1}{k^2x^2}
\end{align*}
\)
Finally, plug in \(v = \dfrac{y}{x}\) and simplify:
\(
\begin{align*}
1 - \dfrac{2y}{x} &= k^2 x^2\\
-\dfrac{2y}{x} &= k^2 x^2 - 1\\
-2y &= x(k^2x^2 - 1)\\
y &= \dfrac{x(1 - k^2x^2)}{2}
\end{align*}
\)
We finally have a solution:
\(
y = \dfrac{x(1 - k^2x^2)}{2}
\)
I think it's time to deal with the caterpillars now.
Solving Gus' Feral Caterpillar Problem
 If you recall, Gus' garden has been infested with caterpillars, and they are eating his cabbages. He's modelled the situation using the differential equation:
If you recall, Gus' garden has been infested with caterpillars, and they are eating his cabbages. He's modelled the situation using the differential equation:
\(
\dfrac{d \text{cabbage}}{dt} = \dfrac{ \text{cabbage}}{t},
\)
where \(t\) is the time in days after the initial infestation. He knows that \(6\) cabbage leaves were eaten on the first day after the infestation,
and wants to know how many cabbage leaves will be eaten on day \(2\). He needs to solve the differential equation, work out the value of \(A\), and plug
in \(t = 2\).
First, we need to check that Gus' equation is homogeneous. Let \(k\) be a real number. Then
\(
\dfrac{k\text{cabbage}}{kt} = \dfrac{\text{cabbage}}{t},
\)
so it certainly is!
Next do the substitution \(\text{cabbage} = vt\), so \( \dfrac{d \text{cabbage}}{dt} = v + t \; \dfrac{dv}{dt}\):
\(
v + t \; \dfrac{dv}{dt} = \dfrac{vt}{t} = v
\)
Subtracting \(v\) from both sides gives:
\(
t \; \dfrac{dv}{dt} = 0,
\)
which is a bit of a let-down, really. So either \(t = 0\), or \(\dfrac{dv}{dt} = 0\). Since time
doesn't stand still, we must have \(\dfrac{dv}{dt} = 0\). This differential equation is particularly
easy to solve. It just says that \(v = C\) for some constant \(C\).
Now, let's substitute back in for \(v\). Since \(\text{cabbage} = vt\), \(v = \dfrac{\text{cabbage}}{t}\)
and so, the solution is:
\(
\begin{align*}
\dfrac{\text{cabbage}}{t} &= C\\
\text{cabbage} &= Ct.
\end{align*}
\)
Finally, plug in the initial condition to find the value of \(C\)
We plug in \(t = 1\) as we know that \(6\) leaves were eaten on day \(1\)
\(
\text{cabbage}(1) = 6 = C(1) = C
\)
So \(C = 6\), and the particular solution to Gus' equation is
\(
\text{cabbage}(t) = 6t.
\)
That will eventually be a lot of cabbage. No wonder Gus is so worried!
On day \(2\) after the infestation, the caterpillars will eat \(\text{cabbage}(2) = 6(2) = 12 \text{ leaves}.\)
Poor Gus!
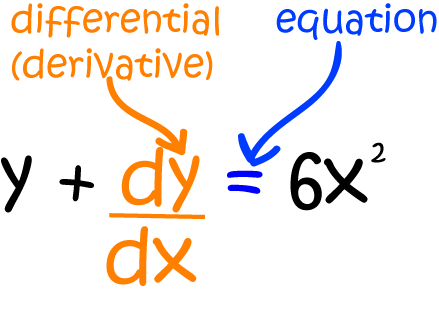
 A plague of feral caterpillars has started to attack the cabbages in Gus the snail's garden. Gus observes that the cabbage leaves
are being eaten at the rate
A plague of feral caterpillars has started to attack the cabbages in Gus the snail's garden. Gus observes that the cabbage leaves
are being eaten at the rate
 If you recall, Gus' garden has been infested with caterpillars, and they are eating his cabbages. He's modelled the situation using the differential equation:
If you recall, Gus' garden has been infested with caterpillars, and they are eating his cabbages. He's modelled the situation using the differential equation: