Using Taylor Series to Approximate Functions

Sam is conducting an experiment. He's interested in the rate of decay of a banana that he left in his lunch box at the end of last term. He decides to use the exponential decay function

to model the amount of banana left after \(t\) days. He plans to compare the mass of banana remaining with the values given by his function each day. However, he has lost his calculator, and wants to find a way to calculate the values of his function with pen and paper.

Luckily, we can approximate functions like \(e^x\) using Taylor series. Taylor series can be thought of as polynomials with an infinite number of terms. To approximate function values, we just evaluate the sum of the first few terms of the Taylor series. For nicely behaved functions, taking more terms of the Taylor series will give a better approximation.

Example:

The Taylor series of \(y = e^x\) is

Taylor's theorem tells us that the function \(y = e^x\) is equal to the infinite sum \( 1 + x + \dfrac{x^2}{2!} + \dfrac{x^3}{3!} + \dots \) for all values of \(x\). Recall that \(n!\) is equal to \(n \times (n-1) \times (n - 2)\times \dots \times 1\).

Let's try some approximations of \(e^x\) at \(x = 1\) using this Taylor series. We should expect that the values will eventually match up with \(e = 2.71828\dots\).

Number of Terms	Part of Taylor Series	Value at \(x=1\)
1	1	1
2	\(1 + x\)	2
3	\(1 + x + \dfrac{x^2}{2!}\)	2.5
4	\(1 + x + \dfrac{x^2}{2!} + \dfrac{x^3}{3!}\)	2.66667
5	\(1 + x + \dfrac{x^2}{2!} + \dfrac{x^3}{3!} + \dfrac{x^4}{4!}\)	2.70833

You can see that the approximations are getting closer and closer to \(e = 2.71828\dots\).

Commonly Used Taylor Series

Functions like \(\sin x\) and \(\cos x\) are commonly used in signal processing, so it's important to be able to approximate them. Here is a list of a few commonly used functions, and their Taylor series.

Function	Taylor Series	Taylor Series in Summation Notation
\(e^x\)	\(1 + x + \dfrac{x^2}{2!} + \dfrac{x^3}{3!} + \dots \)	\(\displaystyle{\sum_{n = 0}^{\infty} \frac{x^n}{n!}}\)
\(e^{-x}\)	\(1 - x + \dfrac{x^2}{2!} - \dfrac{x^3}{3!} + \dots \)	\(\displaystyle{\sum_{n = 0}^{\infty}\frac{(-1)^n }{n!}\;x^n}\)
\(\sin x\)	\(x - \dfrac{x^3}{3!} + \dfrac{x^5}{5!} - \dots \)	\(\displaystyle{\sum_{n = 0}^{\infty}\frac{(-1)^n }{(2n + 1)!}\;x^{2n + 1}}\)
\(\cos x\)	\(1 - \dfrac{x^2}{2!} + \dfrac{x^4}{4!} - \dots \)	\(\displaystyle{\sum_{n = 0}^{\infty}\frac{(-1)^n }{(2n)!}\;x^{2n}}\)
\(\dfrac{1}{1 - x}\) for \(|x|	\(1 + x + x^2 + x^3 + \dots\)	\(\displaystyle{\sum_{n = 0}^\infty x^n}\)

Of course, these are only a few of the many possible Taylor series that can be used to approximate functions.

Looking at the Approximations Graphically

As I said earlier, you can use the first few terms of the Taylor Series of a function to approximate it. If you take more terms, and the function behaves properly, you get a better approximation.

Let's see this in action on the graph of \(y = \sin x\). At each step, the red graph is the graph of \(\sin x\) and the blue graph is the graph of the Taylor Series approximation.

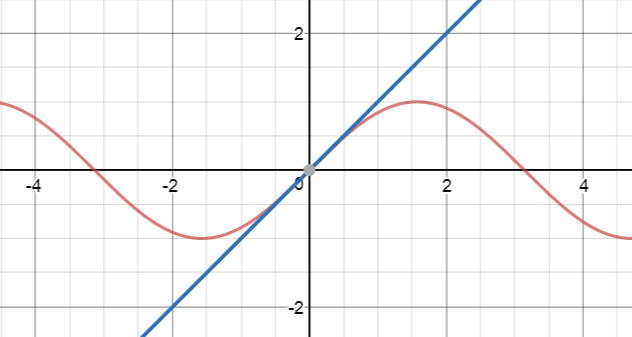
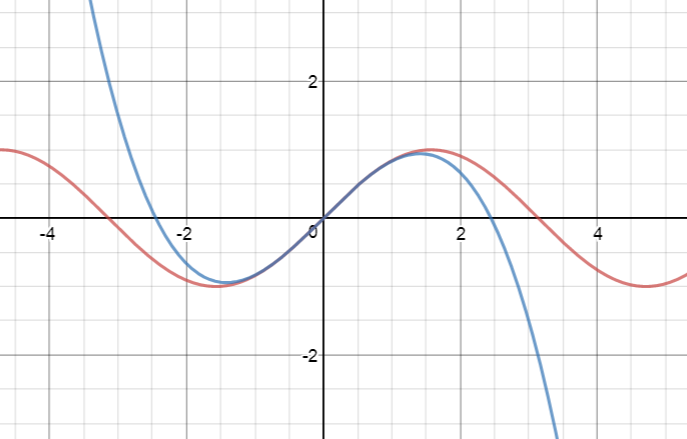
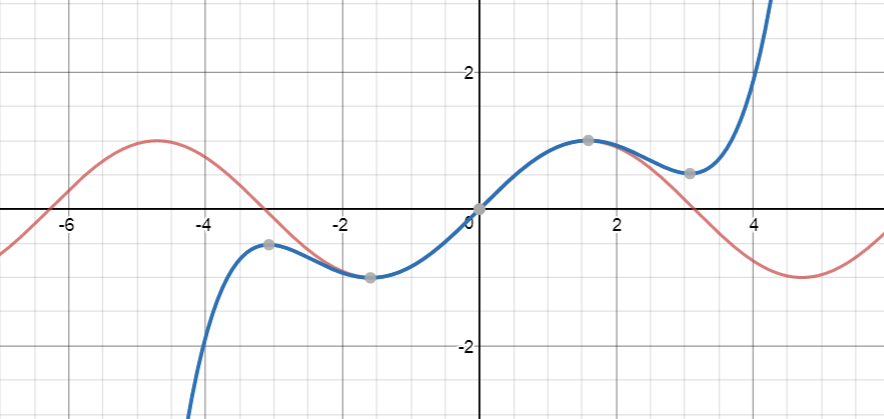
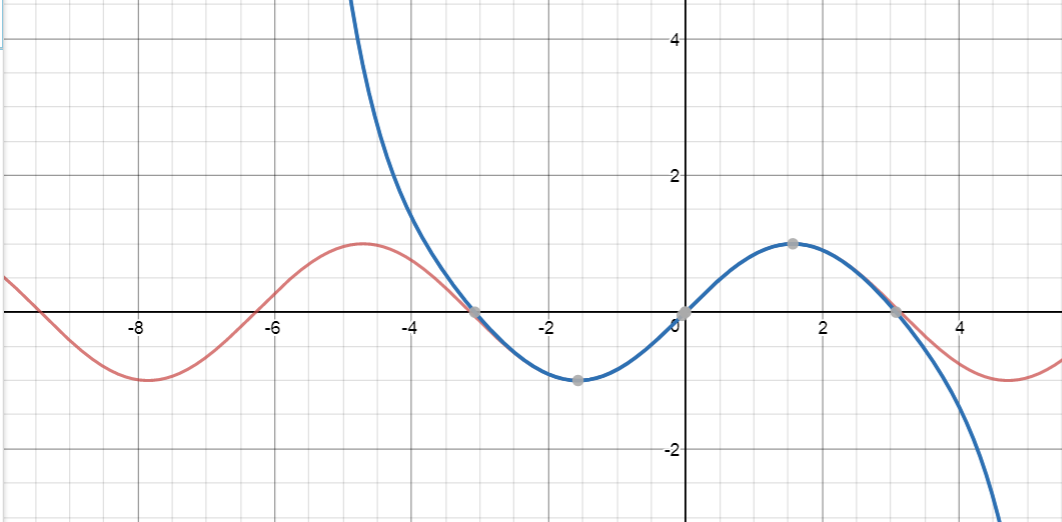
How do we find these polynomials?

This idea was thought up by some very clever people: a Scottish mathematician, James Gregory, and an English mathematician, Brook Taylor, back in the 18th Century. There's nothing very mysterious about finding Taylor series, just a number of steps to follow:

1. Decide you'd like to find a series to approximate your function: \(f(a) = c_0 + c_1(x - a) + c_2 (x - a)^2 + \dots\).
2. Choose a value of \(a\).
3. Use derivatives to work out the values of \(c_0,c_1,c_2,\dots\).

See, there's nothing to it! Well, maybe we need to do a bit of work. Let's have a look at the procedure in more detail:

To find \(c_0\), set \(x = a\). Then our infinite series approximation collapses to

because all the terms involving \((x - a)\) vanish.

Now, we need to find \(c_1\). We take the derivative of both sides of our infinite series approximation:

Next, we plug in \(x = a\). All those pesky terms with \((x - a)\) in them will vanish, and we'll be left with

To find \(c_2\), we need to take the derivative again:

Setting \(x = a\) yields so that

We should start to see a pattern now. The coefficient \(c_n\) is found by

• taking the \(n\)th derivative \(f^{(n)}(a)\) and
• dividing it by the product of the powers of all the preceding terms (i.e. \(n! = n \times (n-1) \times \dots \times 2\times 1\)).

So the Taylor series is and we have a way of building our very own Taylor series:

Example: The Taylor Series for \(\sin(x)\)

Let's start with

and fill in the blanks. We need to find lots of derivatives of \(\sin(x)\). That's actually much easier than it sounds because the derivative of \(\sin x\) is \(\cos x\) and the derivative of \(\cos x\) is \( - \sin x\), so the derivatives we need go through a cycle:

• \(f'(x) = \cos x\)
• \(f''(x) = -\sin x\)
• \(f'''(x) = - \cos x \)
• \(f^{(iv)}(x) = \sin x\)

and we start all over again...
So, our series looks like: Now we need to choose a value for \(a\). A commonly chosen value is \(a = 0\). This would give \(\sin(0) = 0\) and \(\cos(0) = 1\), so it's a good choice. Let's see what this does to our series:

Do you notice how all the terms with even powers of \(x\) have vanished? This is good because \(\sin (x) \) is an odd function, so we'd expect its polynomial approximations to include only odd powers of \(x\). Take a look at the article on odd and even functions if you feel like you need a refresher on these important types of functions.

Stuff for you to do:

Why not have a go at finding the Taylor Series of \(\cos x\) and \(e^x\)? It will help you to fix these ideas in your head.

Historical Note:

Taylor Series with \(a = 0\) are often called Maclaurin Series after the Scottish mathematician, Colin Maclaurin who did a great deal of work with them in the 18th Century.

Oh, and what about Sam? He can use a few terms of the Taylor Series for \(e^{-x}\) and multiply them by 2. He can then plug in \(x = \dfrac{d}{2}\) to approximate the amount of his banana that's left on day \(d\). However, both his mum and I agree that it's better to eat the banana in the first place or, at the very least, to throw it out as soon as it goes mouldy.