Second Derivatives of Functions

If the second word of the title of this article doesn't make any sense to you, it would be a good idea to read the articles on derivatives first, and then come back to this one.

The derivative of a function gives you the slope of the function at any point where it is defined. It measures the rate of change of the function - how fast it is increasing or decreasing at that point.

The second derivative of a function is found by differentiating its derivative. How's that for a tongue-twister? So it's a derivative too, and it measures the rate of change of the derivative. To find the second derivative of the function \(f(x)\):

• Find the derivative \(f'(x)\) of \(f(x)\)
• Take the derivative of \(f'(x)\)

We often use the notation \(f''(x)\) (pronounced f double prime) for the second derivative. The notation \(\dfrac{d^2 y}{dx^2}\) is also commonly used for the second derivative of \(y\) with respect to \(x\).

Example

Find the second derivative of \(f(x) = x^5 + x^2\).

The rules of differentiation tell us that the derivative of \(x^5\) is \(5x^4\), and the derivative of \(x^2\) is \(2x\). So, the derivative of \(f\) is \(f'(x) = 5x^4 + 6x\).

The derivative of \(x^4\) is \(4x^3\), and the derivative of \(x\) is \(1\), so the second derivative of \(f(x)\) is:

Using the alternative notation, we have

• \(y = x^5 + x^2\)
• \(\dfrac{dy}{dx} = 5x^4 + 2x\)
• \(\dfrac{d^2y}{dx^2} = 20x^3 + 2\)

Applications of Calculus to the Physical World

This sounds like the chapter of a maths textbook. What we really want to talk about is distance, speed and acceleration. These are common real-world applications of first and second derivatives.

Example: Gus the snail

Gus the snail is in training to beat the world land-speed record. It will be hard work, but Gus is determined!

Gus tears along a garden path at the impressive speed of \(3 \text{ nanometres}\) every minute:

There are a few different quantities that are important for Gus to determine.

Distance: Gus needs to know how far he has moved along his garden path. Physicists often use the letter \(s\) to denote distance.

To measure the distance Gus has travelled, we'll use the following units and notation:

• distance (in nanometres): \(s\)
• time (in minutes): \(t\)

Speed: It is very important for Gus to work out how much his distance \(s\) changes over time. This is represented by the first derivative of \(s\) with respect to time: \(\dfrac{ds}{dt}\).

Gus's initial speed is \(3 \text{ nanometres per minute}\), so \(\dfrac{ds}{dt} = 3 \text{ nm/min}\)

Acceleration: If Gus wants that land-speed record, he'd better start moving more quickly! He increases his speed to \(4 \text{ nanometres per minute}\) over the next two minutes: Acceleration is the change in speed over time. It's the rate of change of the derivative \(\dfrac{ds}{dt}\), so it is represented by the second derivative \(\dfrac{d^2s}{dt^2}\).

Gus's speed increases by \(1 \text{ nm/min}\) over 2 minutes, so his acceleration is \(\dfrac{d^2s}{dt^2} = \dfrac{1}{2} = 0.5 \text{ nm/min}^2\).

Note: Gus's speed changes by \(0.5\) nanometres per minute per minute. This is more usually written as \( \text{ nm/min}^2\).

More generally,

Quantity	Expression	Value from the Example
Distance	\(s\)	\(3 \text{ nm}\)
Speed	\(\dfrac{ds}{dt}\)	\( 3 \text{ nm/min}\)
Acceleration	\(\dfrac{d^2s}{dt^2}\)	\( 0.5 \text{ nm/min}^2\)

Note: The third derivative tells us how acceleration changes with time, and is found by differentiating the second derivative. It is sometimes called "jerk" or "jolt".

Some examples of graphs and their first and second derivatives

Let's finish with some examples of graphs of functions \(f(x)\), and their first \(f'(x)\) and second \(f''(x)\) derivatives.

Example 1

The picture below shows the graphs of \(f(x) = x^3\) in red, its first derivative \(f'(x) = 3x^2\) in blue and its second derivative \(f''(x) = 6x\) in green.

Example 2

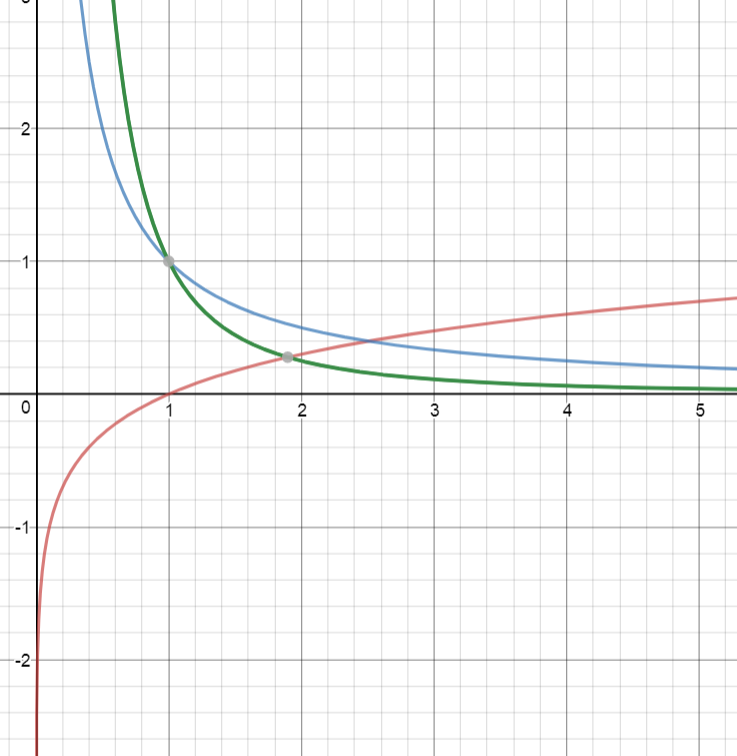
The picture below shows the graphs of \(f(x) = \log(x)\) on the domain \((0,\infty)\) in red, its first derivative \(f'(x) = \dfrac{1}{x}\) in blue and its second derivative \(f''(x) = \dfrac{1}{x^2}\) in green.