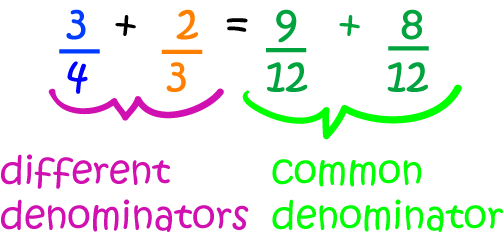
The least common denominator of a group of \(2\) or more fractions is the smallest number that can be used as the denominator of all of the fractions in the group.

Just a few reminders:

• The "denominator" is the number on the bottom of a fraction.
• A "common denominator" occurs when the bottom number of all of the fractions in the group is the same.
• The "least common denominator" is the smallest out of all of the positive numbers that can be used as common denominators for all of the fractions in the group.

For example, let's find the least common denominator of the fractions \(\dfrac{1}{4}\) and \(\dfrac{2}{3}\).

\(\dfrac{1}{4}\) can be written as \(\dfrac{1}{4}\), \(\dfrac{2}{8}\), \(\dfrac{3}{12}\), \(\dfrac{4}{16}\), and so on.

\(\dfrac{2}{3}\) can be written as \(\dfrac{4}{6}\), \(\dfrac{8}{12}\), \(\dfrac{12}{18}\), and so on.

The first fractions from the two lists that have the same denominator are \(\dfrac{3}{12}\) and \(\dfrac{8}{12}\). So, the least common denominator of \(\dfrac{1}{4}\) and \(\dfrac{3}{12}\) is \(12\).

Finding the least common denominator makes it much easier to add and subtract fractions.

For example,