Roman Numerals

You've seen Roman Numerals before. They're the funny collections of \(\text{X}\)s, \(\text{I}\)s, \(\text{M}\)s, \(\text{C}\)s, \(\text{D}\)s and \(\text{L}\)s that crop up at the ends of movies. You might have seen them when your parents made you watch the credits so that they could find out which actor played a particular role. Other places you might have seen them are on clocks, sun dials or old buildings. The picture to the left shows Roman numerals that were used to number a gate at the Coliseum in Rome. In this case, the ancient Romans gave the gate the number \(52\), or \(\text{LII}\).

So what do these funny symbols mean?

Different Roman Numerals are formed by making combinations of the following symbols:

Rules for Combining Symbols to Make New Numbers

• If you want to make a symbol larger, put a smaller symbol to its right (when a symbol appears after a symbol with a larger value, we add it to the larger value.)
• If you want ot make a symbol smaller, put a smaller symbol to its left (when a symbol appears before a symbol with a larger value, we subtract it from the smaller value.)
• Never put more than three of the same symbol one after the other.

Note:Sometimes clock manufacturers break this last rule and write \(4\) as \(\text{IIII}\) to make their clocks look more symmetric.

Examples:

1. How do we write \(4\) in Roman Numerals?
   The nearest symbol to \(4\) is \(\text{V}\), which stands for \(5\). We need to subtract one from \(5\) to get \(4\), so we put the symbol \(\text{I}\) for \(1\) to its left, to give \(4 = \text{IV}\).
2. How do we write \(6\) in Roman Numerals?
   The nearest symbol to \(6\) is \(\text{V}\), which stands for \(5\). We need to add one to \(5\) to get \(6\), so we put the symbol \(\text{I}\) for \(1\) to the right of the \(\text{V}\), to give \(6 = \text{VI}\).
3. How do we write \(48\) in Roman Numerals?
   \(40\) is 10 less than 50, so we have to subtract 10. We write this as \(\text{XL}\), with the \(\text{X}\) (10) to the left of the \(\text{L}\) (50). Now, \(8\) is 2 less than 10, but it's also 3 more than 5. We'd prefer to add things than subtract them, and we're allowed to write three \(\text{I}\)s in a row, so we write \(8 = 5 + 1 + 1 + 1\) as \(\text{VIII}\), with three \(\text{I}\)s to the right of the \(\text{V}\).
4. How do we write \(49\) in Roman Numerals?
   \(49\) is just 1 less than 50, so we can subtract 1 from 50. This means we write a \(\text{I}\) (for 1) to the left of an \(\text{L}\) (for 50). So, \(49 = 50 - 1\) is written as \(\text{IL}\).

How about going back the other way? You just follow the same rules. Don't forget to look back at your table of values for the Roman symbols. Let's look at a couple of examples.

1. \(\text{XI} = 10 + 1 = 11\) because the smaller number \(\text{I}\) (1) is to the right of the \(\text{X}\).
2. \(\text{XC} = 100 - 10 = 90\) because the smaller number \(\text{X}\) (10) is to the left of the larger number \(\text{C}\) (100), and so must be subtracted from it.
3. \(\text{XLVIII} = 50 - 10 + 5 + 1 + 1 + 1 = 48\). The smaller number \(\text{X}\) (10) is to the left of the larger number \(\text{L}\) (50) and so must be subtracted. The three \(\text{I}\)s are to the right of the larger number \(\text{V}\) (5), and must be added to it.

Some Commonly Used Combinations of Roman Numerals

Here are some of the more common combinations of Roman numerals that you might see up on buildings or at the cinema.

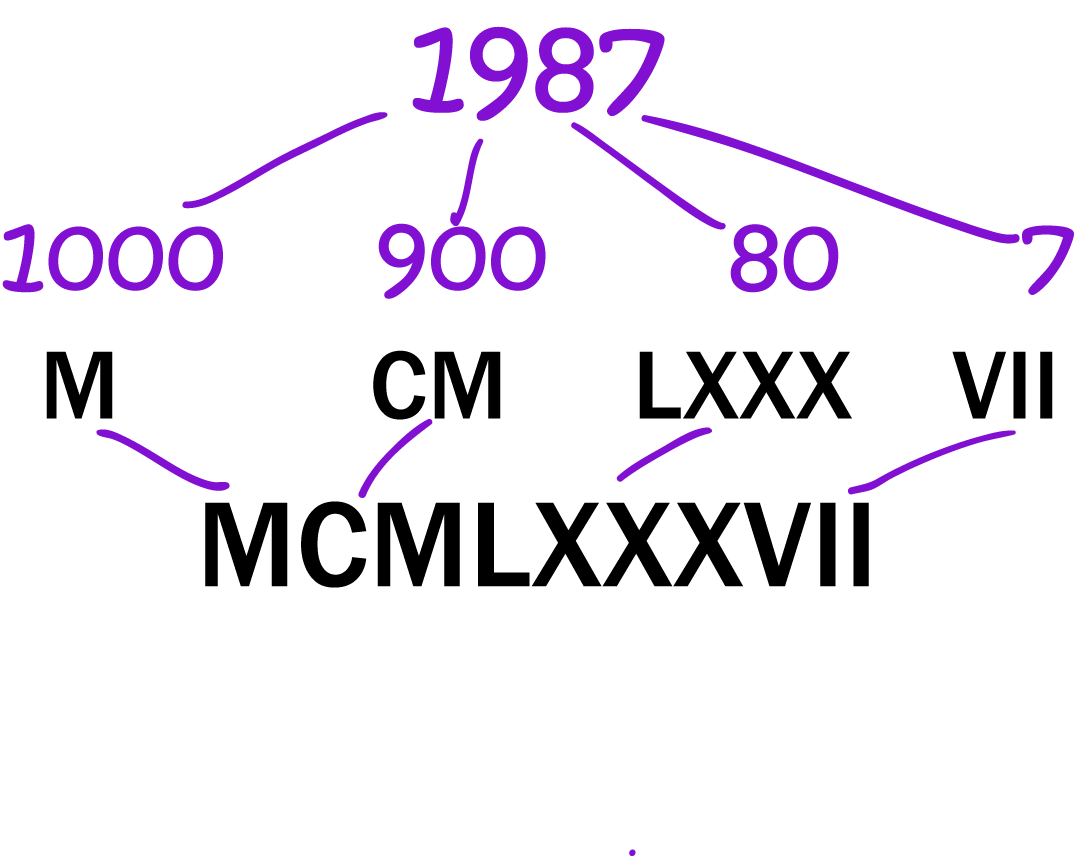
Let's Write the Year at the End of a Movie

There must have been at least one good movie made in 1987. Let's see how this year would appear in the credits of a movie.

Write 1987 as \(1,000 + 900 + 80 + 7\) and write each bit in Roman numerals:

• \(1000 = \text{M}\)
• \(900 = \text{CM}\)
• \(80 = \text{LXXX}\)
• \(7 = \text{VII}\)

Now glue it all together to give \(1987 = 1,000 + 900 + 80 + 7 = \text{MCMLXXXVII}\).

How Do You Remember the Symbols for Roman Numerals?

Probably the hardest thing about writing and reading Roman numerals is remembering what all the symbols mean. Here's something that might help you.

OK, so now you're all set. Tomorrow, you'll be able to take out your sun-dial and tell the time in a flash! Provided, of course, that it isn't raining.